1.
 変わる里山：北摂の絵図と地図にみる景観変化
2.
 　

3.

 　 物質科学へのアインシュタインの功績
4.
 　 この世で最も重い原子を求めて
　
5.
 　 漢方薬ナビゲーション：時空を超えて科学する心
6.
 　 宇宙から見た世界の雷活動
　
7.
 　 太陽エネルギーの有効利用
　
8.
 　 繰り返しから生まれる複雑さ
　
9.
 　 ナノテクの4次元空間＝ナノ３次元+アト秒
10.
 　 PDBj: Protein Data Bank japan (日本蛋白質構造データバンク)
11.
 　 時を止め、空間を作る
　
12.
 　 琥珀にひそむ時空のなぞ
　
13.
 　 時間と空間の知覚：知と行動の科学
14.
 　 曲面の世界
　
15.
 　 出版活動
　
14. 曲面の世界

サイエンスクラブ ／ 林　俊成
地球儀
皆さんは、身の周りにある物はまっすぐな物でできていると思っていませんか？しかし、私達の住む地球は球ですね。

あまりにも身近なため気付きにくいかもしれませんが、私達は球の表面で暮らしているのです。球の表面は曲面の一つですが、曲面の世界では私達の常識とは違う法則があります。

そんな身近にありながらあまり知らない曲面の世界を紹介していきたいと思います。
内角の和が180°ではない三角形
下の図を見てください。

赤道上のある地点から北極点へまっすぐ進み、北極点で右に90°曲がってまっすぐ進み、赤道に着いたら右に90°曲がって進むと、元の地点に戻ってきます。

これによって描かれた三角形では、内角の和が90°＋90°＋90°＝270°。つまり、球面上の三角形の内角の和は180°ではないのです。
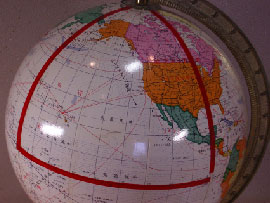
地球儀による説明図（1）
地球儀による説明図（2）
どの距離が短い？
下の左図を見てください。球面上の青、緑、赤どれが短いと思いますか？緑が一番短いように見えるかもしれませんが、実際には青が一番短いのです。緑は緯度線と平行に引いているため、平面上なら緑が一番短くなりますが、球面上では平面とは異なってくるのです。　　　　　　　
距離の説明図（1）
 距離の説明図（2）
角度から三角形の面積が分かる？
普通三角形の面積は　底辺×高さ÷２のように、辺の長さが必要ですね。しかし、球面上では球の半径と三角形の内角の和だけで、三角形の面積が求まるのです。（三角形の内角の和−π）×半径×半径 が、三角形の面積です。
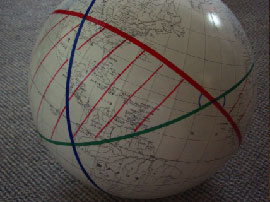
地球儀による三角形の面積（1） 地球儀による三角形の面積（2）
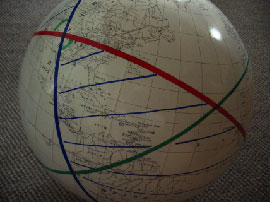
地球儀による三角形の面積（3） 　 地球儀による三角形の面積（4）
曲面の世界では、私たちの常識とは異なる点がたくさんあるのです。